Introduction to Meshing In FEA
- Why the choices in meshing matter
- Element Shapes
- Meshing Algorithm
- Mesh Uniformity and Size
- Element Order
- Integration Order
- Partitioning
- Conclusion
Meshing is often a pain point and bottleneck for FEA analysts. With so many shapes, sizes, and options to choose from, it can be daunting to new users. I remember teaching an Abaqus Introductory course and seeing the wide eyes and open mouths of the engineers as I went through the library of elements one can choose from. Even FEA veterans can struggle with meshing. To say its more an art than a science is an understatement! In fact, many points and tips that are given by me or commercial software is often based on empirical results rather than theoretical ones.
Meshing is a key step in ensuring that your model not only runs in a feasible amount of time but also solve your equations in accurately which is why so much of an FEA analyst time is spent on getting the mesh just right!
This guide is meant to be an introductory approach to meshing for FEA. A lot of handwavy, non-technical reasons are given as to why we have certain rules of thumbs (and links better explaining the theoretical reasons).
TLDR:
| Element Shape | Square/Hexahedral elements are generally better and computationally more efficient |
|---|---|
| Meshing Algorithms | Try and obtain a Structured or swept mesh for better model runtime.
If meshing is too difficult use unstructured meshing approach instead |
| Mesh Uniformity and Size | Aim to have elements where the element lengths are all roughly the same size (e.g. squares and cubes).
Always start with a courser mesh before refining. |
| Element Order | Use Quad/Hex Linear or Quadratic Tets/Tri elements for general purpose and initial starting point.
Use higher order elements for smoother problems e.g. bending problems |
| Integration Order | Use Reduced order elements when available as computationally cheap and many packages contain hourglass control.
If hourglassing is present, try full order. |
| Partitioning | Break down a complex region into ‘simple’ regions (e.g. prisms, cylinders) and complex regions (e.g. joint intersections, corners and geometry with holes).
Partitioning is your best tool in controlling the meshing algorithm! |
Why the choices in meshing matter
Simply put the speed, accuracy and convergence of our models depends significantly on our meshing choices! You want to be playing the game of trying to use the least amount of effort (i.e. number of elements) to
When we want to simulate how one of our CAD designs behaves under some load case with FEA, we first must discretize our model into a series of simple shapes such as squares and triangles glued together. However, this discretization is not unique – there are all kinds of shapes and sizes that can meet our need. This is kind of like how different Lego blocks can be used to build the same statue.
If we are given unlimited time, the size and number of elements wouldn’t matter. But when we add the constraint that we want the model to be accurate but also as fast as possible, choosing the correct size and shape can make all the difference.
A second thing to why meshing matters is that the shape and properties of each element often introduces additional terms into our equations. This is a result of the discretization process. A well-known example is numerical viscosity that is introduced when discretizing fluid equations. We’ll discuss some of these in later chapters.
Element Shapes
In FEA there are a wide library of shapes. We’ll focus on 4 main element shapes that are used in 2D and 3D domains (There are others such as wedge elements, but we’ll ignore them for now and 1D elements aren’t well… that hard to mesh!):
2D Elements:
Quadrilaterals Elements (Quads)
Triangular Elements (Tri)
3D Elements:
Hexahedral Elements (Hex)
Tetrahedral elements (Tets)
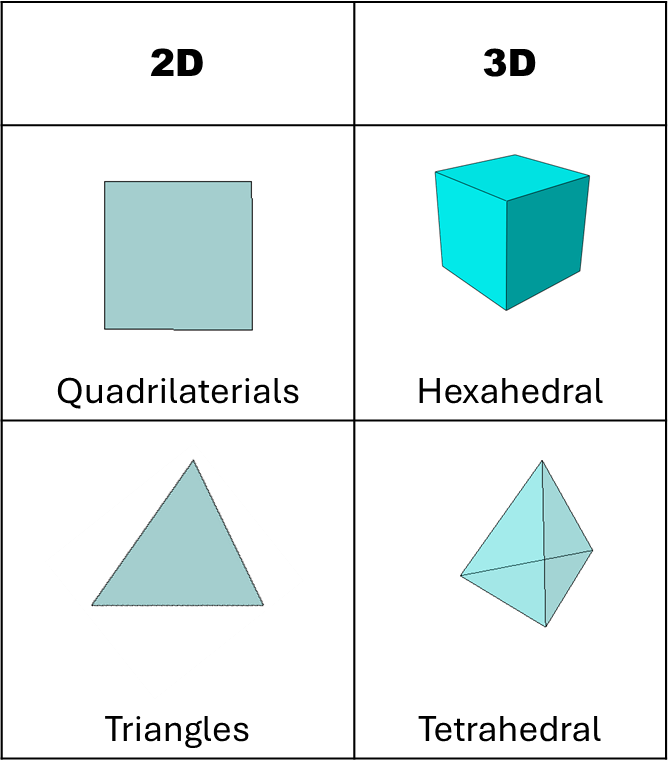
In a perfect world, it shouldn’t matter which elements, but we don’t live in that world! The choices really come down between time spent meshing vs time spent solving the model:
| Tetrahedral/Triangular Elements | Quadrilaterals/Hexahedral |
|---|---|
+ Easy Meshing + Can better capture curves + Can always Mesh model | + Fewer elements need to model geometry. + Resulting in faster solve time + Better accuracy |
| - Greater number of DOFs compared to Quad/Hex elements for same geometry | - Can be difficult to mesh geometry especially highly curved surfaces - May be impossible to mesh with these elements |
So, when choosing the element shape, one should try and mesh with Hex/Quad elements first. But If the geometry just does not allow it, then resort to using tets/tri elements.
Meshing Algorithm
In the previous chapter, I mentioned that sometimes the geometry won’t allow you to mesh with certain elements. This could be (but not limited to) the following:
The geometry was imported from an external CAD program and is not perfect, so the meshing software has difficulty understanding the geometry (This is especially the case with complex curved surfaces and geometries)
Element shapes may require certain rules to be met before the geometry can be meshed with them.
Well focus on the latter point in this section. Furthermore, for 2D surfaces, Quads and Tri elements can join making them straightforward to mesh. For the remainder of this chapter, we’ll talk about meshing 3D objects.
There are generally 3 types of automatic meshing methods:
Structured or Mapped
Unstructured or Free
Swept/Mixed Structured – unstructured.
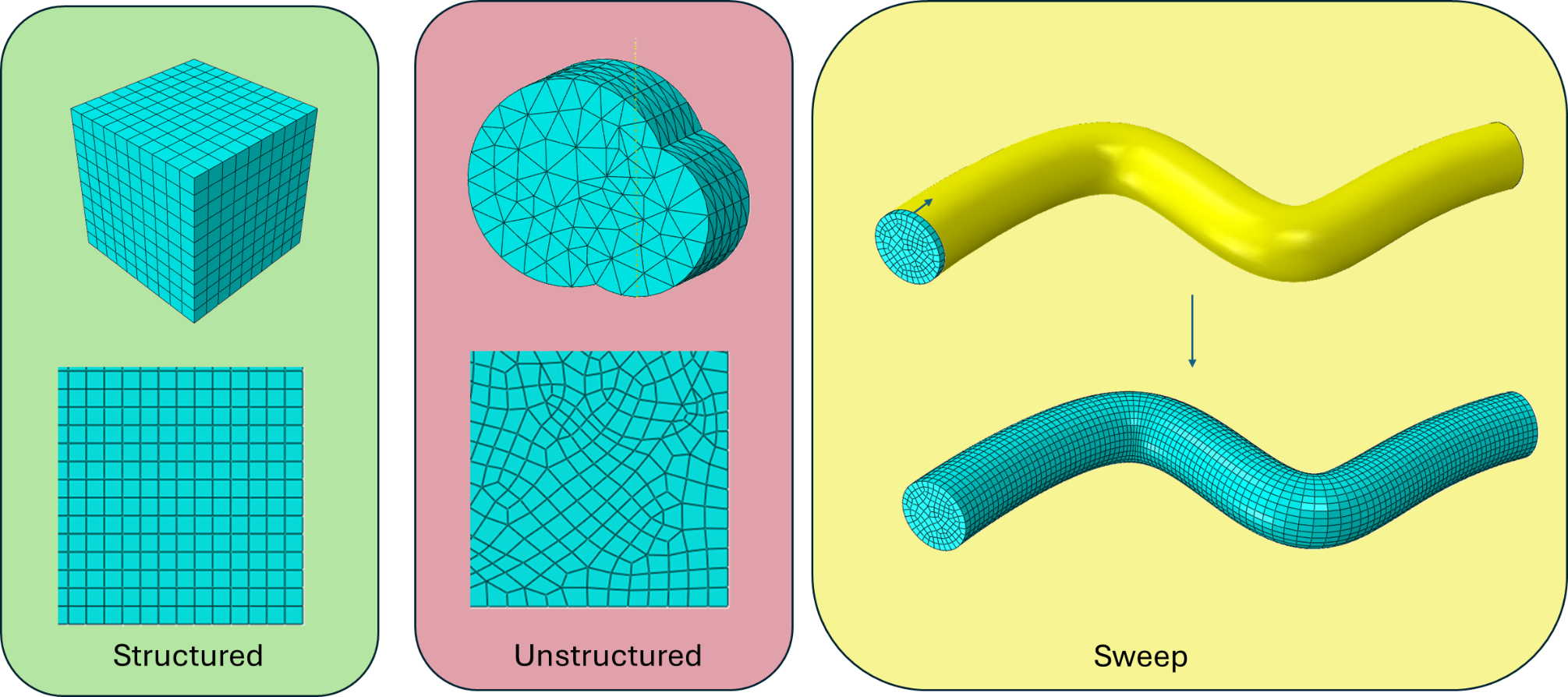
Hexahedral elements tend to only be meshable through structured and sweep meshing algorithms while tetrahedral elements are more flexible and can be meshed using any of the methods. As a rule of thumb, you should always try and get a structured mesh followed by a swept mesh. If this is too difficult or time consuming, use an unstructured mesh.
Structured
Structured meshes have some sort of regular arrangement and connectivity between elements. A chessboard being made of 8x8 smaller squares is an example of a structured mesh. In FEA, structured meshes are the best type of mesh you can go for as it can improve convergence, accuracy, and runtime of models. However, because of their regularity, structured meshes are often limited to specific geometric shapes. An example of this requirement in Abaqus meshing is that structured meshing cannot be applied to geometry with holes in them. To get around this we can partition the geometry (discussed in a later section) so instead of 1 region with a hole, we create 4 smaller regions that have no hole (but together form the original geometry).
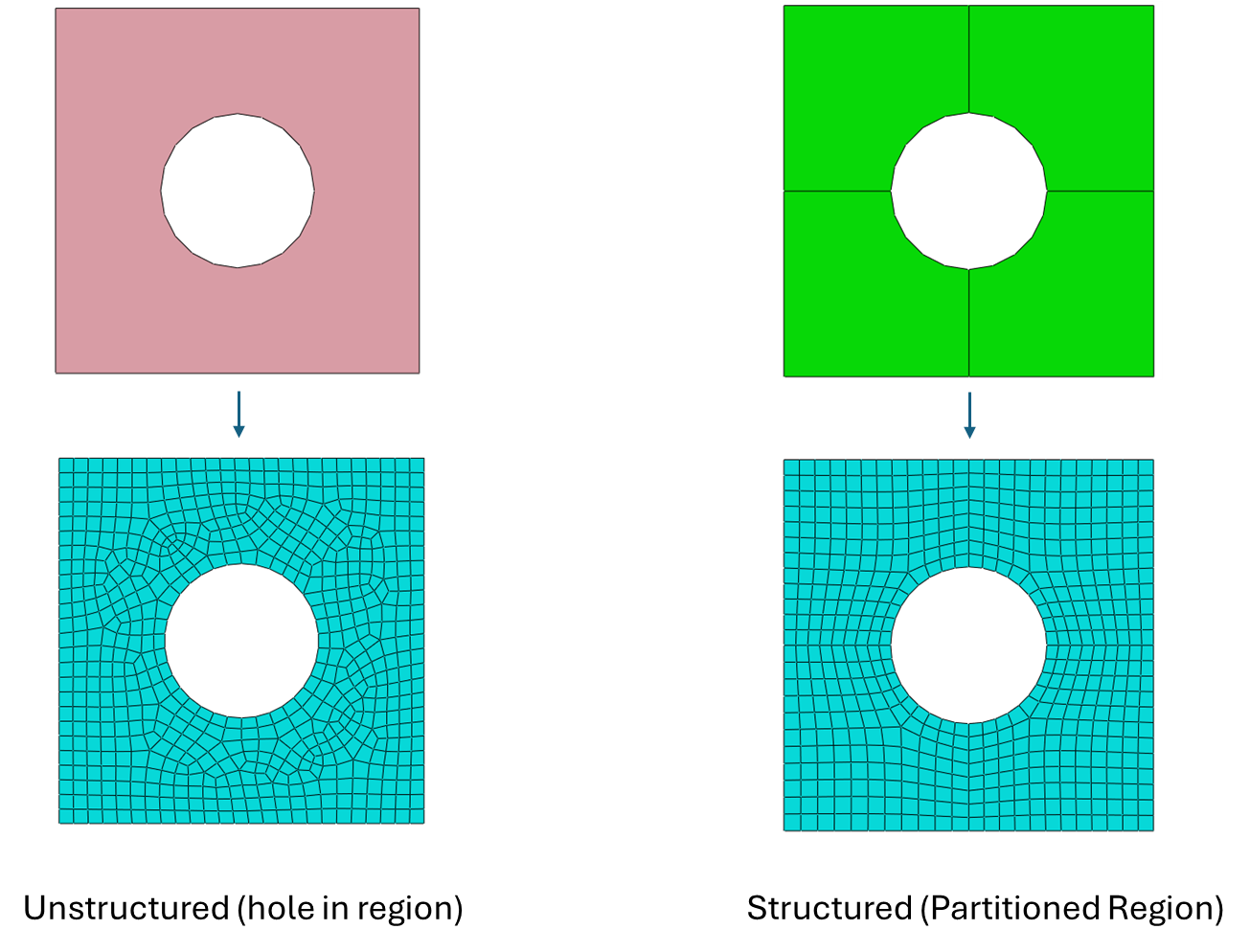
Structured meshing only works on simple regions, such as rectangular prisms, so for more complex regions, aim to partition the complex regions into smaller, more simple regions without any holes. The links here and here, For Abaqus’ documentation gives a great explanation for this (you’ll need to create a free account to see this)
Unstructured
Unstructured meshes are of course the opposite to structured meshes: the elements and their connectivity is irregular and can’t be expressed in some nice way like a grid. The advantage of unstructured meshes is they are geometry agnostic meaning they can mesh any shape without needing to partition or modify the geometry. Sometimes unstructured meshing is the only way to mesh highly complex structures or problematic geometry.
Essentially, unstructured meshing is geometry independent and significantly easier and faster process than structured meshing. However, the flip side is that unstructured meshes tend to have longer run times than their structure or swept counterparts.
Swept
Finally, we have swept meshing which is like an in-between of structured and unstructured meshing. A swept mesh first starts by picking a ‘source’ face to mesh and then extruding this face along some predetermined path. For those CAD users, it is analogous to how the sweep geometry creation tool works in that you sketch some cross-sectional face and then extrude along some path. You can see it in the image above where the initial face is meshed and then swept along some path.
Swept meshes fall under a mix between unstructured and structured meshing as the mesh orthogonal to the swept path can be unstructured while the meshing along the swept path is a form of structured meshing. Swept meshing is great in geometries that are derived from extrusions and sweeps such as pipes.
Mesh Uniformity and Size
You may have noticed that the ‘good’ meshes you’ve seen in the previous images look quite pleasing to look at. This is seriously a good rule of thumb to follow! In meshing we try to aim for 2 things:
Shape Uniformity
Elements to capture features such as curved surfaces.
Here shape Uniformity roughly means we want elements whose element lengths/dimensions to all be the same. This means that elements have no ‘preferred’ direction. What this means is that when meshing you want to aim for elements with squares/ equilateral triangles for 2D meshing and cube/regular tetrahedral. This can be hard to achieve when we want to include details at small scales such as fillets, so you’ll often have to implement mesh refinement around smaller details and then transition it to larger sized elements.
Furthermore, highly deformed elements (i.e the ratio between the longest edge and shortest edge is very large) often are less accurate and can even produce convergence errors. Many FEA/meshing software provide metrics (such as aspect ratio, skew angles etc) to help provide metrics on the quality of your mesh to keep this in check.
Next, we have the number of elements we need. Again this is super dependent on your model but there’s two points I would say if you are starting off:
Start with a mesh as course as possible
Try and use just enough elements to capture the feature
The first point is very important. Many people make the mistake of going straight into a very fine. This is problematic for two reasons: the first is that it could be a waste of computing i.e you did not need a mesh this fine but more importantly, it’s very common to make a mistake to make a mistake during model setup such as forgetting the load or putting in the wrong values. These errors can only manifest when running the model so having a run with a course model can be extremely useful to set up. It also can give you an idea of the behaviour of the model.
The second point is definitely on the art side of meshing. Being able to use the least amount elements needed to capture your results takes years of experience and understanding of what you are modelling. However, I find that if, at a glance, the feature looks to be well captured by the discretization then that’s a good starting point. Remember, if you are always unsure, always run the model with a courser mesh and rerun with a finer mesh if necessary.
Element Order
In FEA, we interpolate the values of interest (such as displacement or velocity) within an element. The interpolation/element order we choose is up to us. Generally, we use polynomial interpolation. Typically, we choose a low order either linear, quadratic or cubic interpolation. For orders higher than linear, we often add ‘midnodes’ – nodes that are along the edge of elements not just at each element vertex:
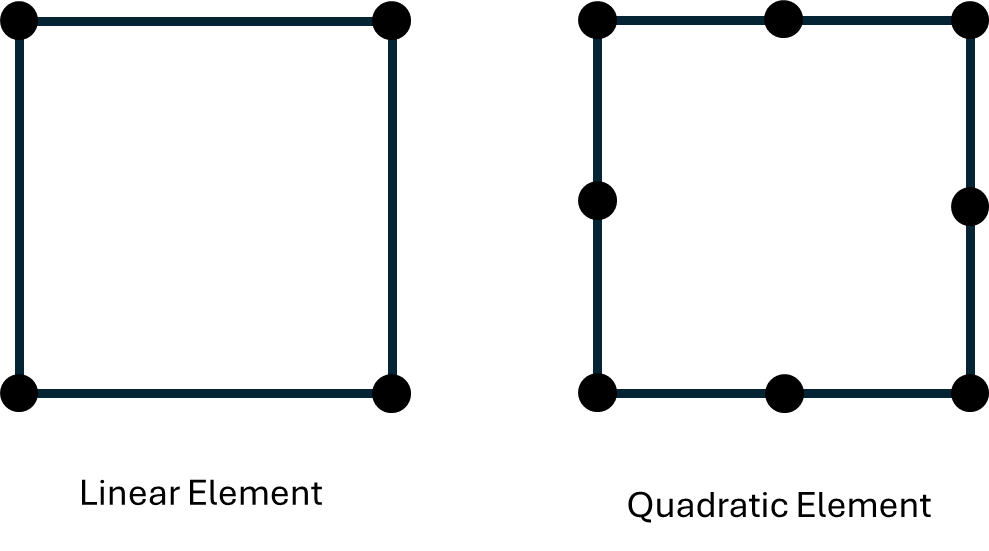

Generally speaking, higher order interpolation schemes give smoother and more accurate results and so require less elements to achieve the same level of accuracy. An example of this is quadratic order elements being more accurate than linear elements in bending problems. However, linear elements tend to be more applicable to a wide range of problems such as models with contact (which are inherently non-smooth). Linear elements also perform better is in high deformation simulations where elements can become very irregular and deformed. This sort of makes sense as in high deformation and contact models, results aren’t necessarily smooth (think about the crumpling in a car crash) so assuming a level of smoothness isn’t the best here.
The method of interpolation can also change the behaviour of our elements e.g. linear element tend to be stiffer than quadratic elements. In the case for tri and tet elements we tend to always use quadratic order over linear order as quadratic tri/tet elements have better stiffness properties.
So in summary, higher order elements are generally better for smoother problems, while linear elements are cheaper and more general purpose and can be used in high deformation models. When in doubt linear elements should be used first (exception are tri/tet elements where you should use quadratic elements)
Integration Order
When we solve our FEA equations, we need to integrate over each element’s volume. To do this we often use gaussian quadrature. Gaussian quadrature gives a way of integrating our interpolation functions (which are normally polynomials) by evaluating the polynomials at special points called ‘gauss points’ or in FEA material points. In the image below these points are represented as the x’s inside the element. Using a special set of weightings and points, we can exactly compute the integral of a polynomial function assuming the element is regular shaped (e.g. cubes and squares shaped elements). This is called ‘Fully’ integrated elements (in that these elements exactly compute the integral of the finite element). We can also use less points in each direction for more efficient calculations in return for a higher integration error. In this case these elements are ‘reduced’ order elements.
Just like element order and shape, integration order can affect the stiffness/behaviour of our elements. In fact, depending on the integration scheme, we generate 2 common artifacts:
Shear-locking for Fully integrated elements.
Hourglassing for reduced order elements
In fact, there are cases where the fully integrated elements do worse than reduced order elements! So more is not necessarily better!
Shear locking occurs in fully integrated linear elements. This effect causes elements to be to stiff during bending. This is essentially due to linear element edges not being able to bend/curve. Quadratic elements can bend as you they have a mid node as seen above. Reduced order elements also do not experience shear locking.
Hourglassing is an effect that can occur in reduced order elements. This occurs during bending and creates can create an hourglassing effect as seen below. The cause of this is that the single integration point in the reduced element, in a sense, can’t ‘detect’ certain bending modes and so no strain energy is generated. In other words, reduced elements can suddenly deform into these hourglass shapes seemingly at their own will. These modes of deformations are called zero-energy modes and can quickly propagate throughout the mesh giving useless results. From the image below, you can see the hourglass shapes the elements form in the top right corner. Fortunately, this problem can be identified, and many FEA codes have implemented way to avoid this issue, with so called hourglass control. This is done by injecting a little but of artificial stiffness to prevent the deformation without affecting the results significantly (generally hourglass control only contributes less than 5% of the total energy of the system).
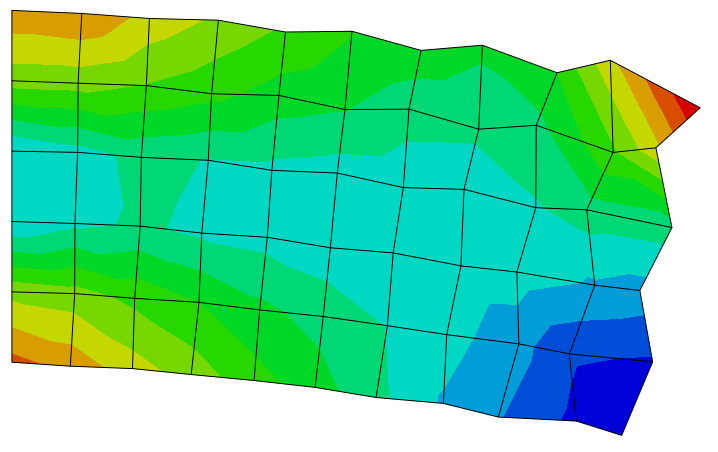
When choosing the initial element, always start with a reduced order element if you can. These are cheaper than fully integrated elements and most codes provide hourglass control.
Partitioning
In the previous sections, we’ve mainly talked in relation to geometries that are easy to mesh such as rectangles and circles. However, in the real world most geometries are complex with many twists and turns such as turbine blades or engine blocks. These complicated geometries can make many meshing algorithms fail to do a good job. Even if we use unstructured meshing algorithms, we can still get a poor mesh as the geometry may have small features and details that can interfere with the meshing algorithm. This is where partitioning comes into play. Partitioning is breaking down your geometry from one single region into a set of smaller connected regions. Partitioning provides boundaries that can help steer the meshing algorithm into the mesh that you desire. An example we saw earlier was the square plate with a hole in the centre. Another example is the lug in the image below. If we leave the lug as is, we get an alright mesh. However, you can see that the left side of lug is essentially a rectangular prism meaning that region is a prime candidate for structured mesh. And so if we partition the lug so that we create two regions, one side as the rectangular prism and the other side with the hole, we can achieve a much more uniform mesh. We could partition the geometry further to get an even more symmetrical and better mesh.
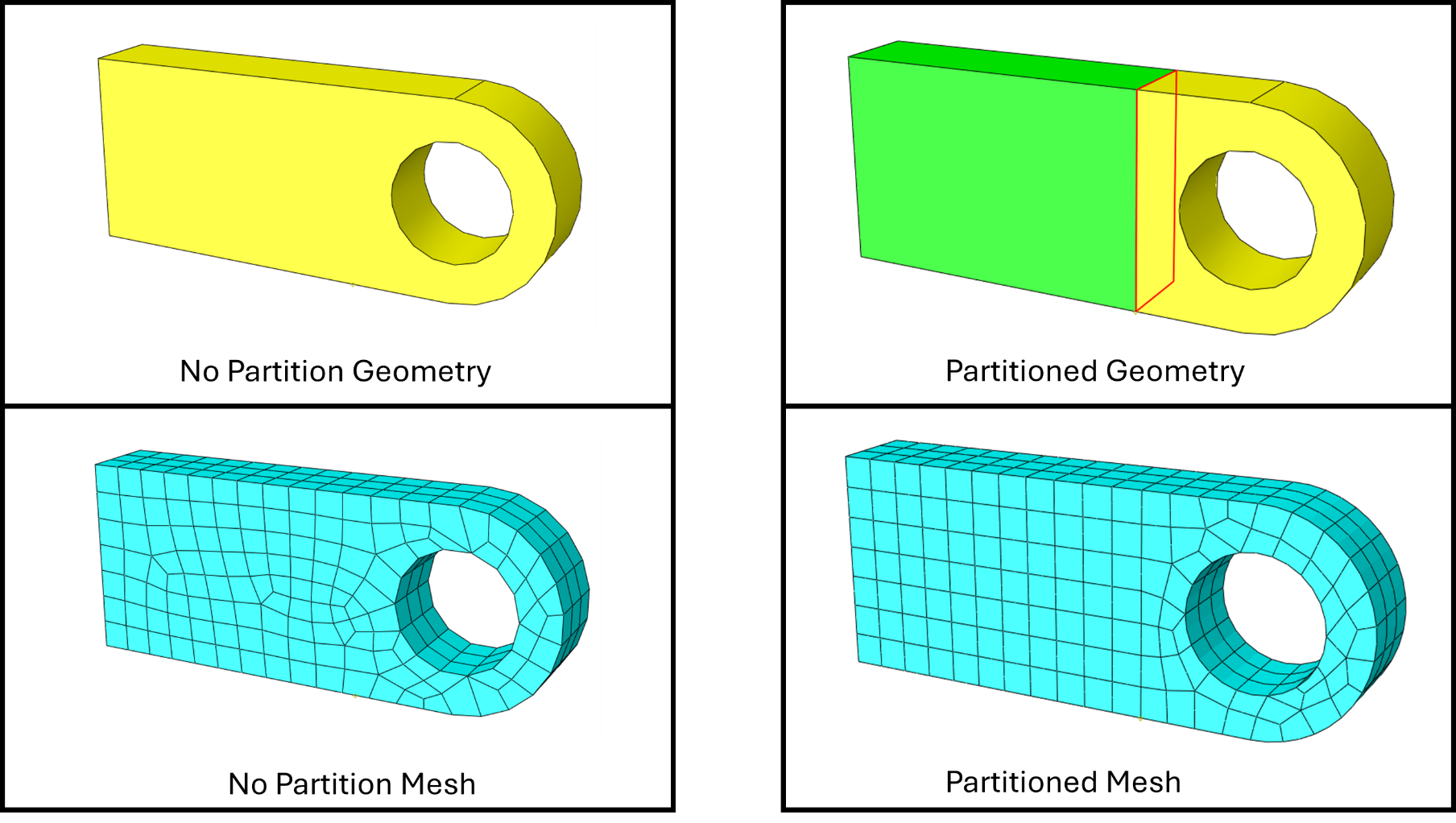
The advice I have for partitioning is to try and separate regions into ‘simple’ regions (e.g. extrusions, plates) and complicated regions first (e.g. joint intersections, corners, holes). You can also use partitioning to break down complicated regions into ‘simpler’ regions such as the hole in the plate example above. For many packages partitioning is your best tool in controlling the meshing algorithm!
Conclusion
That does it for my introduction to meshing. There’s still a huge sea of other stuff to consider (e.g. shell and beam elements, material properties, loads etc) when making an effective model but meshing really is the bottleneck you will often face in using FEA in a commercial setting as it can make or break a model. Many tips I have learnt is much more from an empirical approach rather than a theoretical one. And also, be ready to break these tips! These tips are good if you are new or creating a new model. If you are modelling a scenario where you have familiarity, then ignore my advice! If you have any questions or comments then please let me know!
If you need a recap here’s a summary of the main tips to look out for:
| Element Shape | Square/Hexahedral elements are generally better and computationally more efficient |
|---|---|
| Meshing Algorithms | Try and obtain a Structured or swept mesh for better model runtime.
If meshing is too difficult use unstructured meshing approach instead |
| Mesh Uniformity and Size | Aim to have elements where the element lengths are all roughly the same size (e.g. squares and cubes).
Always start with a courser mesh before refining. |
| Element Order | Use Quad/Hex Linear or Quadratic Tets/Tri elements for general purpose and initial starting point.
Use higher order elements for smoother problems e.g. bending problems |
| Integration Order | Use Reduced order elements when available as computationally cheap and many packages contain hourglass control.
If hourglassing is present, try full order. |
| Partitioning | Break down a complex region into ‘simple’ regions (e.g. prisms, cylinders) and complex regions (e.g. joint intersections, corners and geometry with holes).
Partitioning is your best tool in controlling the meshing algorithm! |

